Development of the derivative of the error function

Notice that we've defined the squared error to be

Error = \frac{1}{2} (y - \hat{y})^2.

Also, we've defined the prediction to be

\hat{y} = w_1 x + w_2.

So to calculate the derivative of the Error with respect to
w_1
, we simply use the chain rule:

\frac{\partial}{\partial w_1} Error = \frac{\partial Error}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial w_i}.

The first factor of the right hand side is the derivative of the Error with respect to the prediction
\hat{y}, which is
-(y-\hat{y}).

The second factor is the derivative of the prediction with respect to
w_1, which is simply
x.

Therefore, the derivative is

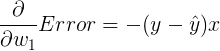
Exercise

Calculate the derivative of the Error with respect to
w_2
and verify that it is precisely
-(y-\hat{y}).